1671. Minimum Number of Removals to Make Mountain Array
1671. Minimum Number of Removals to Make Mountain Array
Tag: monotone-stack, DP, No AC first time
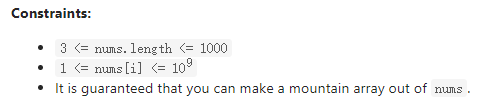
Description

Solution
For each index, we can calculate its preceding minimum delete number and its succeeding delete number. Then search for the minimum sum.
So how to calculate deleting number? -> calculate longest monotonous sequence
- A naive way, use DP to calculate: Find the very nums[j] that lower than nums[i], then inherit its by length + 1
1 | dp[i] = max(dp[j] + 1) for all nums[j] < nums[i] |
- A more efficient way is to maintain a monotone-stack, and greedily replace the very nums[j] that exact greater than nums[i]. Example:
1 | 1 3 5 7 4 |
So that we can maximally insert number into this monotone-stack which means can get the longest sequence.
Code
1 | class Solution { |
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.

